
The point of this section is to make some of the mathematics as clear as possible: How exactly does Music Algorithms produce its results in terms of mapping sequences of numbers to pitches?
In general, the Modulo Operation takes an interval of numbers (such as a chunk of a sequence) and maps this interval to a range of pitches. The mapping can be thought of as a transformation in terms of “wrapping” using modular arithmetic. The modulo is determined by the pitch range and a couple of examples are provided:
Note: This section assumes familiarity with modular arithmetic. For example, it is assumed the reader understands how “7 Mod 4” is 3, or that “48 Mod 12” is 0, etc. Often, curricula might refer to this as “Clock Arithmetic” (using Mod 12). As a basic definition, two numbers A and B are said to be “equal” or “congruent” modulo N if and only if their difference (A – B) is exactly divisible by N.In which case we could write A = B (Mod N). Taking remainders, such as 34 divided by 6 is five with a remainder of 4. Note that “34 Mod 6” = 4.
Example 1
[A] Consider the first eight Fibonacci Numbers (0, 1, 1, 2, 3, 5, 8, 13). The interval defined by these numbers goes from 0 – 13, so the interval width is 13 { That is, 13 minus 0, or the maximum value minus the minimum value in general }
[B] Suppose we want to map those eight numbers in [A] to a range of pitches that goes from 20 – 26, and note that the width of the pitch range is 6 { 26 minus 20 }. This means we are operating in Mod 7 since there are 7 pitches in that range from 20 to 26, inclusive.
[C] Here’s how the Fibonacci Numbers in [A], get mapped to pitch range in
- You’ll have to calculate each (Fibonacci Number) Mod 7
- Here’s how the end result would look:
Fibonacci Numbers: 0 , 1, 1, 2, 3, 5, 8,13 …become mapped to…
Pitches: 20, 21,21,22,23,25,21,26 - What follows below is a step-by-step analysis of how just one of the Fibonacci Numbers (8), got mapped to the Pitch of { 21 } in this example:
- Our Pitch Interval is (20-26), so we have Mod 7
- We know that 8 Mod 7 is 1
- 20 + 1 is 21
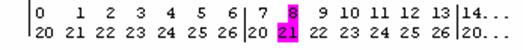
Example 2
[A] Consider the ninth through the sixteenth Fibonacci numbers (21, 34, 55, 89, 144, 233, 377, 610).The interval defined by these numbers goes from 21 – 610, so the interval width is 589 { 610 minus 21}.
[B] Suppose we want to map those eight numbers in [A] to a range of pitches that goes from 27 – 32, and note that the width of the pitch range is 5 { 32 minus 27 }. This means we are operating in Mod 6 since there are 6 pitches in that range from 27 to 32, inclusive.
[C] Here’s how the Fibonacci Numbers in [A], get mapped to pitch range in [B]:
- You’ll have to calculate each (Fibonacci Number) Mod 6
- Here’s how the end result would look:
Fibonacci Numbers: 21,34,55,89,144,233,377,610 …become mapped to…
Pitches: 30,31,28,32, 27, 32, 32, 31 - What follows below is a step-by-step analysis of how just one of the Fibonacci Numbers (34), got mapped to the Pitch of { 31 } in this example:
- Our Pitch Interval is (27-32), so we have Mod 6
- We know that 34 Mod 6 is 4
- 27 + 4 is 31


